python去噪函数_Python | 简单的扩音，音频去噪，静音剪切

发布日期：2022/10/19 11:52:13      浏览量：

原标题：Python | 简单的扩音，音频去噪，静音剪切

之前一段时间一直在搞数字语音识别，在训练算法上耗费了很多时间，但结果不尽人意。后来才发现自己一直忽视了音频预处理的一步，于是转而囫囵吞枣般学习一些简单的信号处理算法。这里简单介绍一下以下内容：

扩音

音频去噪

静音剪切

文末将会给出源代码和demo代码的git库地址，有需要的同学请自取。

基本概念

数字信号

数字信号是通过对连续的模拟信号采样得到的离散的函数。它可以简单看作一个以时间为下标的数组。比如，x[n]，n为整数。比如下图是一个正弦信号(n=0,1, ..., 9)：

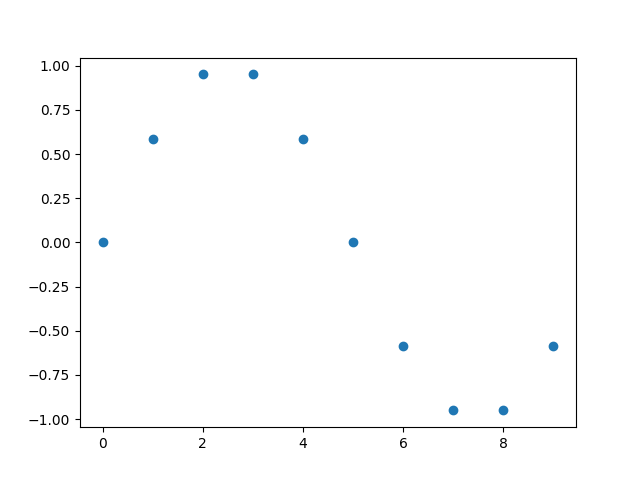
对于任何的音频文件，实际上都是用这种存储方式，比如，下面是对应英文单词“skip”的一段信号(只不过由于点太多，笔者把点用直线连接了起来）：

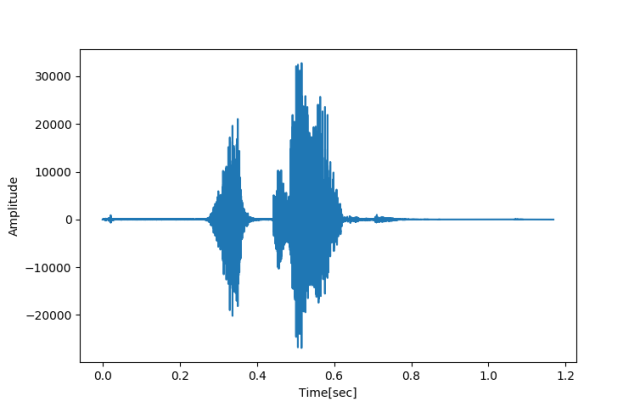
衡量数字信号的能量（强度），只要简单的求振幅平方和即可：

E = sum(x[n]*x[n])

频率

我们知道，声音可以看作是不同频率的正弦信号叠加。那么给定一个声音信号（如上图），怎么能够知道这个信号在不同频率区段上的强度呢？答案是使用离散傅里叶变换。对信号x[n], n=0, ..., N-1，通常记它的离散傅里叶变换为X[n]，它是一个复值函数。

比如，对上述英文单词“skip”对应的信号做离散傅里叶变换，得到它在频域中的图像是：

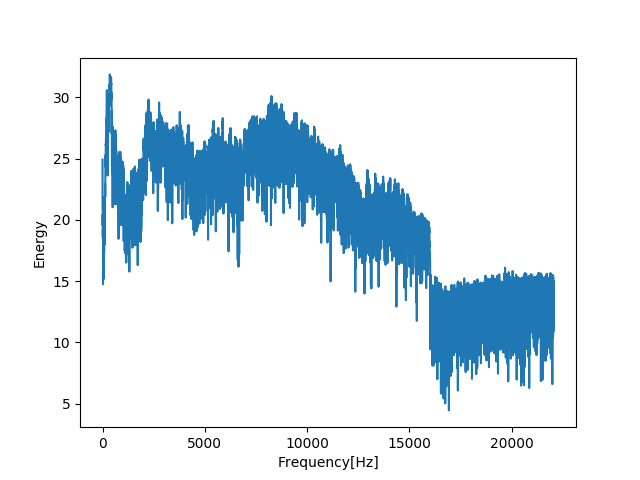
可以看到能量主要集中在中低音部分（约16000Hz以下）。

在频域上，也可以计算信号的强度，因为根据Plancherel定理，有：

E = sum(x[n]*x[n]) = 1/N*sum(|X[n]|*|X[n]|)

分帧

对于一般的语音信号，长度都至少在1秒以上，有时候我们需要把其中比如25毫秒的一小部分单独拿出来研究。将一个信号依次取小段的操作，就称作分帧。技术上，音频分帧是通过给信号加一系列的窗函数实现的。

我们把一种特殊的函数w[n]，称作窗函数，如果对所有的n，有0<=w[n]<=1，且只有有限个n使得w[n]>0。比如去噪要用到的汉宁窗，三角窗。

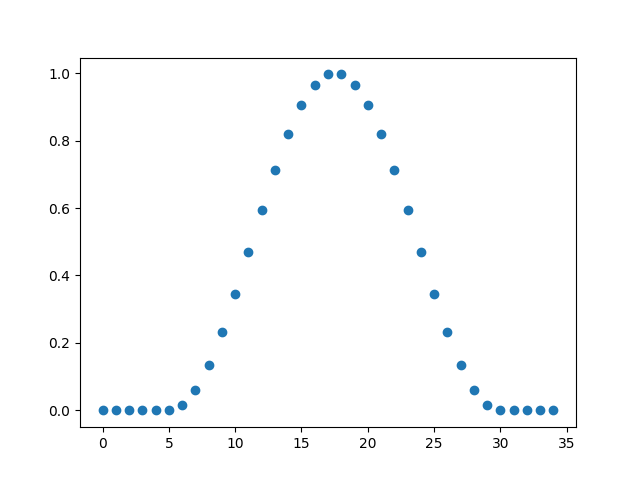
汉宁窗

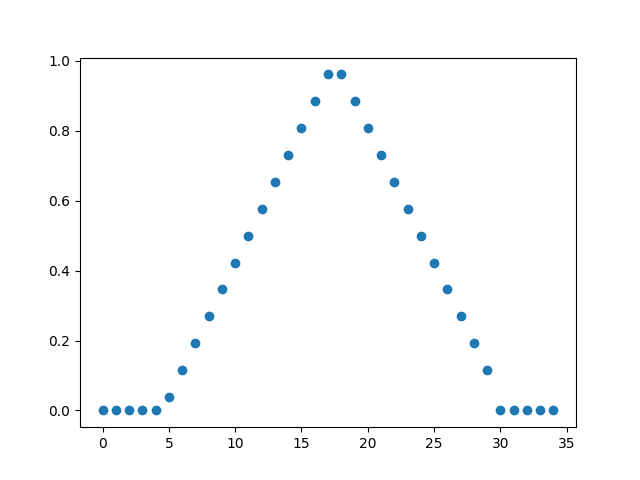
三角窗

我们将平移的窗函数与原始信号相乘，便得到信号的“一帧”：

w[n+d]*x[n]

比如用长22.6毫秒的汉宁窗加到“skip”信号大约中间部位上，得到一帧的信号：

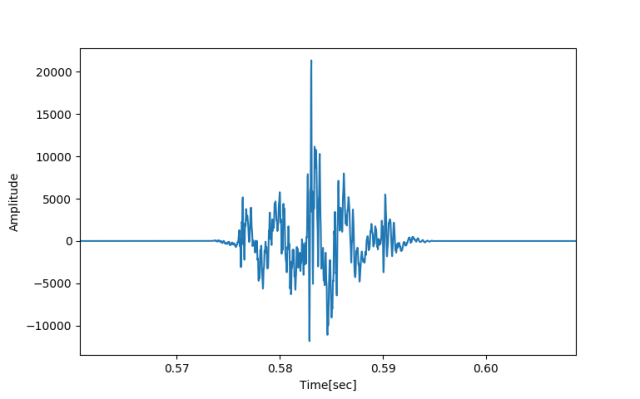
可见除一有限区间之外，加窗后的信号其他部分都是0。

对一帧信号可以施加离散傅里叶变换（也叫短时离散傅里叶变换），来获取信号在这一帧内（通常是很短时间内），有关频率-能量的分布信息。

如果我们把信号按照上述方法分成一帧一帧，又将每一帧用离散傅里叶变换转换到频域中去，最后将各帧在频域的图像拼接起来，用横坐标代表时间，纵坐标代表频率，颜色代表能量强度（比如红色代表高能，蓝色代表低能），那么我们就构造出所谓频谱图。比如上述“skip”发音对应的信号的频谱图是：

（使用5.8毫秒的汉宁窗）

从若干帧信号中，我们又可以恢复出原始信号。只要我们适当选取窗口大小，以及窗口之间的平移距离L，得到 ..., w[n+2L], w[n+L], w[n], w[n-L], w[n-2L], ...，使得对k求和有：

sum(w[n+kL]) = 1

从而简单的叠加各帧信号便可以恢复出原始信号：

sum(x[n]*w[n+kL]) = x[n]

最后，注意窗函数也可以在频域作用到信号上，从而可以起到取出信号的某一频段的作用。

下面简单介绍一下3种音效。

1. 扩音

要扩大信号的强度，只要简单的增大信号的“振幅”。比如给定一个信号x[n]，用a>1去乘，便得到声音更大的增强信号：

a*x[n]

同理，用系数0

2. 去噪（降噪）

对于白噪音，我们可以简单的用“移动平均滤波器”来去除，虽然这也会一定程度降低声音的强度，但效果的确不错。但是，对于成分较为复杂，特别是频段能量分布不均匀的噪声，则需要使用下面的噪声门技术，它可以看作是一种“多带通滤波器”。

这个特效的基本思路是：对一段噪声样本建模，然后降低待降噪信号中噪声的分贝。

更加细节的说，是在信号的若干频段f[1], ..., f[M]上，分别设置噪声门g[1], ..., g[M]，每个门都有一个对应的阈值，分别是t[1], ..., t[M]。这些阈值时根据噪声样本确定的。比如当通过门g[m]的信号强度超过阈值t[m]时，门就会关闭，反之，则会重新打开。最后通过的信号便会只保留下来比噪声强度更大的声音，通常也就是我们想要的声音。

为了避免噪声门的开合造成信号的剧烈变动，笔者使用了sigmoid函数做平滑处理，即噪声门在开-关2个状态之间是连续变化的，信号通过的比率也是在1.0-0.0之间均匀变化的。

实现中，我们用汉宁窗对信号进行分帧。然后对每一帧，又用三角窗将信号分成若干频段。对噪声样本做这样的处理后，可以求出信号每一频段对应的阈值。然后，又对原始信号做这样的处理（分帧+分频），根据每一帧每一频段的信号强度和对应阈值的差（diff = energy-threshold），来计算对应噪声门的开合程度，即通过信号的强度。最后，简单的将各频段，各帧的通过信号叠加起来，便得到了降噪信号。

比如原先的“skip”语音信号频谱图如下：

可以看到有较多杂音（在高频，低频段，蓝色部分）。采集0.25秒之前的声音作为噪声样本，对信号作降噪处理，得到降噪后信号的频谱图如下：

可以明显的看到大部分噪音都被清除了，而语音部分仍完好无损，强度也没有减弱，这是“移动平均滤波器”所做不到的。

3. 静音剪切

在对音频进行上述降噪处理后，我们还可以进一步把多余的静音去除掉。

剪切的原理十分简单。首先用汉宁窗对信号做分帧。如果该帧信号强度过小，则舍去该帧。最后将保留的帧叠加起来，便得到了剪切掉静音部分的信号。

比如，对降噪处理后的“skip”语音信号做静音剪切，得到的新信号的频谱图为：

参考

维基百科词条-噪声门

开源音频处理软件 Audacity （频谱图都是直接用它画的，扩音，降噪，静音剪切这些效果它都有源代码）

我的GitHub