SLAM算法简介

发布日期：2022/1/2 23:57:57      浏览量：

本文的主要目的是简单介绍移动机器人领域中广泛应用的技术SLAM(同步定位与地图绘制)的理论基础以及应用细节。虽然目前存在很多关于SLAM技术的方方面面的论文，但是对于一个新手来说，仍然需要花费大量的时间去调研与把握SLAM发展的脉络。本文希望能够将SLAM技术在保持一些理论基础的前提下，能够按照一种简单易懂的方式呈现出现了。在阅读完本文后，读者应该可以在一个移动机器人上实现最简单使用的SLAM技术。

SLAM可以通过多种方法实现，首先其可以在多种不同的硬件上实现。其次，SLAM更像是一个概念而不是一个算法。SLAM技术包含了许多步骤，其中的每一个步骤均可以使用不同的算法实现。在这里，我们对其中的每一步介绍一种最为常见的方法，至于其他的方法仅作一个简介。

本文的目的是一种非常简单实用的方式将SLAM技术呈现出来，如果读者有一定SLAM技术的技术，可以看出这里提供了一种基于EKF（扩展卡尔曼滤波）的完整的解决方案。需要注意的是，SLAM技术仍然是目前机器人领域的研究热点之一，仍然有许多问题需要深入研究。

1. 关于SLAM

SLAM是同步定位与地图构建(Simultaneous Localization And Mapping)的缩写，最早由Hugh Durrant-Whyte 和 John J.Leonard提出。SLAM主要用于解决移动机器人在未知环境中运行时定位导航与地图构建的问题。

SLAM通常包括如下几个部分，特征提取，数据关联，状态估计，状态更新以及特征更新等。对于其中每个部分，均存在多种方法。针对每个部分，我们将详细解释其中一种方法。在实际使用过程中，读者可以使用其他的方法代替本文中说明的方法。这里，我们以室内环境中运行的移动机器人为例进行说明，读者可以将本文提出的方法应用于其他的环境以及机器人中。

SLAM既可以用于2D运动领域，也可以应用于3D运动领域。这里，我们将仅讨论2D领域内的运动。

2. 机器人平台

在学习SLAM的过程中，机器人平台是很重要的，其中，机器人平台需要可以移动并且至少包含一个测距单元。我们这里主要讨论的是室内轮式机器人，同时主要讨论SLAM的算法实现过程，而并不考虑一些复杂的运动模型如人形机器人。

在选择机器人平台时需要考虑的主要因素包括易用性，定位性能以及价格。定位性能主要衡量机器人仅根据自身的运动对自身位置进行估计的能力。机器人的定位精度应该不超过2%，转向精度不应该超过5%。一般而言，机器人可以在直角坐标系中根据自身的运动估计其自身的位置与转向。

从0开始搭建机器人平台将会是一个耗时的过程，也是没有必要的。我们可以选择一些市场上成熟的机器人开发平台进行我们的开发。这里，我们以一个非常简单的自己开发的机器人开发平台讨论，读者可以选择自己的机器人开发平台。

目前比较常见的测距单元包括激光测距、超声波测距以及图像测距三种。其中，激光测距是最为常用的方式。通常激光测距单元比较精确、高效并且其输出不需要太多的处理。其缺点在于价格一般比较昂贵（目前已经有一些价格比较便宜的激光测距单元）。激光测距单元的另外一个问题是其穿过玻璃平面的问题。另外激光测距单元不能够应用于水下测量。

另外一个常用的测距方式是超声波测距。超生波测距以及声波测距等以及在过去得到十分广泛的应用。相对于激光测距单元，其价格比较便宜；但其测量精度较低。激光测距单元的发射角仅0.25°，因而，激光基本上可以看作直线；相对而言，超声波的发射角达到了30°，因而，其测量精度较差。但在水下，由于其穿透力较强，因而，是最为常用的测距方式。最为常用的超声波测距单元是Polaroid超声波发生器。

第三种常用的测距方式是通过视觉进行测距。传统上来说，通过视觉进行测距需要大量的计算，并且测量结果容易随着光线变化而发生变化。如果机器人运行在光线较暗的房间内，那么视觉测距方法基本上不能使用。但最近几年，已经存在一些解决上述问题的方法。一般而言，视觉测距一般使用双目视觉或者三目视觉方法进行测距。使用视觉方法进行测距，机器人可以更好的像人类一样进行思考。另外，通过视觉方法可以获得相对于激光测距和超声波测距更多的信息。但更过的信息也就意味着更高的处理代价，但随着算法的进步和计算能力的提高，上述信息处理的问题正在慢慢得到解决。

这里，我们使用激光测距方法进行距离测量。其可以很容易实现较高的测量精度并且很容易应用于SLAM中。

3. SLAM的一般过程

SLAM通常包含几个过程，这些过程的最终目的是更新机器人的位置估计信息。由于通过机器人运动估计得到的机器人位置信息通常具有较大的误差，因而，我们不能单纯的依靠机器人运动估计机器人位置信息。在使用机器人运动方程得到机器人位置估计后，我们可以使用测距单元得到的周围环境信息更正机器人的位置。上述更正过程一般通过提取环境特征，然后在机器人运动后重新观测特征的位置实现。SLAM的核心是EKF。EKF用于结合上述信息估计机器人准确位置。上述选取的特征一般称作地标。EKF将持续不断的对上述机器人位置和周围环境中地标位置进行估计。SLAM的一般过程如下图所示：

当机器人运动时，其位置将会发生变化。此时，根据机器人位置传感器的观测，提取得到观测信息中的特征点，然后机器人通过EKF将目前观测到特征点的位置、机器人运动距离、机器人运动前观测到特征点的位置相互结合，对机器人当前位置和当前环境信息进行估计。

下图是估计的详细过程。

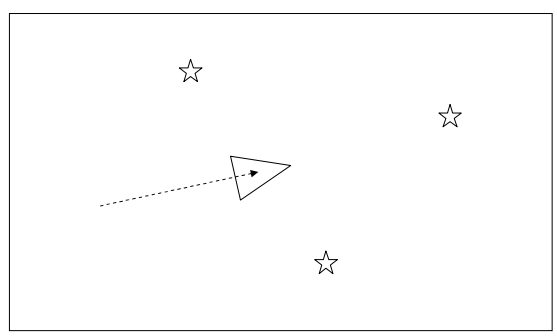上图中三角形表示机器人，星号表示路标；机器人首先使用测距单元测量地标相对于机器人的距离和角度。然后进行开始进行运动，并且到达一个新的位置，机器人根据其运动方程预测其现在所处于的新的位置。

在新的位置，机器人通过测距单元重新测量各个地标相对于机器人的距离和角度，测量得到的距离和角度与上述预测结果可能并不一致，因而，上述预测值可能并不是机器人准确位置。

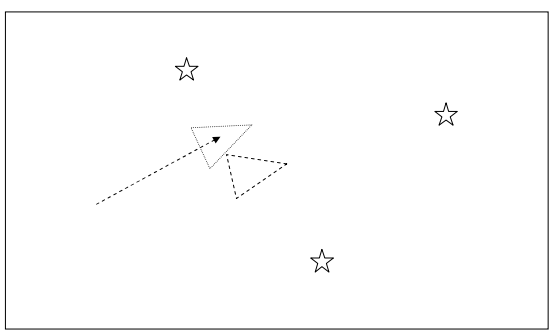在机器人看来，通过传感器获得的信息相对于通过运动方程得到的信息更为准确，因而，机器人将通过传感器的数据更新对机器人位置的预测值，如上图中实线三角形所示(虚线为第一步中通过运动信息预测的机器人位置)。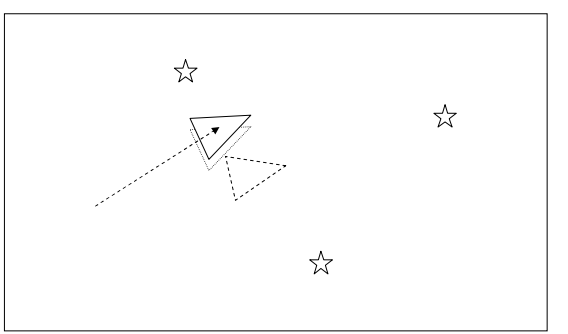

经过上述结合直轴，我们重新估计得到的新的机器人位置如上图实线三角形所示，但由于测距单元精度有限，因而，此时，机器人可能实际处于上图点状三角形位置，但此时估计结果相对于初始预测结果已经有明显的改善。

4. 测距单元

SLAM的第一步需要通过测距单元获取机器人周围环境的信息。这里，我们以激光测距单元为例。以一个常见的激光测距单元为例，其测量范围可到360°，水平分辨率为0.25°，即激光束的角度为0.25°。其输出如下：

2.98，2.99，3.00，3.01，3.02，3.49，3.50，...，2.20，8.17，2.21

激光测距单元的输出表示机器人距最近障碍物的距离。如果由于某些原因，激光测距单元无法测量某个特定角度上的安全范围，那么其将返回一个最大值，这里以8.1为例，测距单元返回数据超过8.1即意味着激光测距单元在该角度上发生测量错误。需要注意的是，激光测距单元可以以很高的频率对周围环境进行测量，其可以实现10-100Hz的全周扫描。

5. 机器人自身运动模型

SLAM的另外一个很重要的数据来源是机器人通过自身运动估计得到的自身位置信息。机器人自身位置数据通过对机器人轮胎运行圈数的估计可以得到机器人自身位置的一个估计，其可以被看作EKF的初始估计数据。

另外一个需要注意的是需要保证机器人自身位置数据与测距单元数据的同步性。为了保证其同步性，一般采用插值的方法对数据进行前处理。由于机器人的运动规律是连续的，因而，一般对机器人自身位置数据进行插值。相对而言，由于测距单元数据的不连续性，因而其插值基本上是不可以实现的。

6. 特征（地标）

地标是环境中易于观测和区分的特征。一般使用这些特征确定机器人位置。我们可以通过下面的方法想象上述工作过程，假设在一个陌生的房间内，闭上眼睛，那么此时我们如何确定自身的位置呢？通常而言，我们将在环境中不断走动，通过触摸物体或者墙壁确定自身位置。上述如被触摸的物体以及墙壁等都可以被看做用于估计自身位置的地标。下面是一些典型的地标。

可以看出，通常而言，对于不同的环境，一般我们选择不同的地标。

一般而言，地标需要满足下面的条件：

1. 地标应该可以从不同的位置和角度观察得到；

2. 地标应该是独一无二的，从而可以很容易的将底边从其他物体中分辨出来

3. 地标不应该过少，从而导致机器人需要花费额外的代价寻找地标；

4. 地标应该是静止的，因而，我们最好不要使用一个人作为地标

举例来说，室内环境中的地标，我们可以选择为墙壁与地面之间的连线，以及墙角等。如下图所示：

7.特征提取

根据上述步骤6确定完需要提取的特征后，我们接下来需要从测距单元获得的信息中准确的提取出我们需要的特征。特征提取的方法有很多种，其主要取决于需要提取特征以及测距单元的类型。

这里，我们将以如何从激光雷达得到的信息提取有效特征为例进行说明。这里，我们使用两种典型的特征提取方法，Spike方法和RANSAC方法。

Spike方法使用极值寻找特征。通过寻找测距单元返回数据中相邻数据差距超过一定范围的点作为特征点。通过这种方法，当测距单元发射的光束从墙壁上反射回来时，测距单元返回的数值为某些值；而当发射光束碰到其他物体并反射回来时，此时测距单元将返回另外一些数值；两者将具有较大的差别。如下图所示：

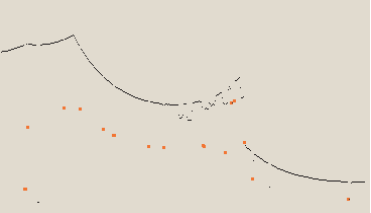图中红点为根据Spike方法提取到的特征。

Spike方法也可以通过下面的步骤实现，对于相邻的三个点A,B,C,分别计算（A-B）与（C-B），然后将两者相加，如果结果超过一定范围，则表示提取到一个特征。

采用Spike方法提取环境特征，需要保证相邻两个激光束照射的物体距离机器人距离之间具有较大的变化，因而，其并不能够适用于光滑环境中的特征提取。

RANSAC（随机采样方法）也可以被用于从激光测距单元返回数据中提取系统特征。其中测距单元返回数据中的直线将被提取为路标。在室内环境中，由于广泛存在墙壁等，因而，在测距单元返回的数据中将存在大量的直线。

RANSAC首先采用随机采样的方法提取测距单元返回数据中的一部分，然后采用最小二乘逼近方法来对上述数据进行拟合。进行数据拟合后，RANSAC方法将会检查测距单元数据在拟合曲线周围的分布情况。如果分布情况满足我们的标准，那么我们就认为机器人看到了一条直线。

在使用EKF估计机器人位置和环境地图时，EKF需要将地标按照距离机器人当前的位置和方位表示出来。我们可以很容易的使用三角几何的方法将提取到的直线转变为固定的特征点，如下图所示：

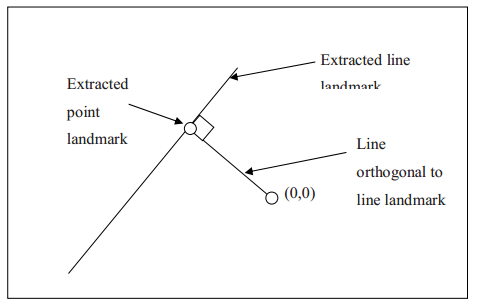
前面我们提到了特征提取的两种不同的方法，Spike方法和RANSAC方法，两者均可以用于室内环境中特征的提出。相比较而言，Spike方法较为简单，并且对室内环境中的活动物体不具有鲁棒性。RANSAC方法通过提取直线的方法提取环境中的特征，相对较为复杂，但对室内活动的物体具有更好的适应性。

8. 数据关联

数据关联是将不同时刻位置传感器提取到的地标信息进行关联的过程，也成为重观察过程。

举例来说，对于我们人类来说，假设我们在一个房间内看到了一把椅子，现在我们离开房间，过一段时间后，再次回到房间，如果我们再次看到了椅子，那么我们可以认为这把椅子很有可能就是我们之前看到的椅子。但是，如果我们假设房价内有两把完全一样的椅子，重复上述过程，当我们再次来到房间后，我们可能无法区分我们看到的两把椅子。但我们可以猜测，此时比如说左边的椅子仍然是之前看到的左边的椅子，而右边的椅子仍然是之前看到的右边的椅子。

在实际应用中进行数据关联时，我们可能遇到下面的问题：

1. 我们可能上一次看到了某个地标，但下一次却没有看到；

2.我们可能这次看到了地标，但之后却再也看不到这个地标；

3.我们可能错误的将现在看到的某个地标与之前看到的某个地标进行关联；

根据我们选择路标时的标准，我们可以很容易的排除上面第1和第2个问题。但对于第三个问题，如果发生了，将会对我们的导航以及地图绘制造成严重的问题。

现在我们将讨论解决上面第三个问题的方法。假设我们现在已经到了每时每刻采集处理得到的路标的方位信息，并将其其中的特征存储在一数据库中。数据库初始阶段是空的，首先我们建立的第一条规则是，除非该特征已经出现了N次，否则我们并不将其加入数据库。当得到一副新的传感器信息后，我们进行下面的计算：

1.得到一副新的传感器信息后，首先利用上面的特征提取方法提取特征；

2.将提取到的特征与数据库中已经出现N次的并且距离最近的特征关联起来；

3.通过验证环节验证上面的关联过程是正确的，如果验证通过，则表明我们再次看到了某个物体，因而其出现次数+1，否则表明我们看到了一个新的特征，在数据库中新建一个特征，并将其记作1.

上述特征关联方法被称作距离最近方法。上面最简单的计算距离的方法是欧式距离的计算，其他距离计算包括马氏距离等，虽然效果更好，但计算结果更为复杂。

验证环节通过利用EKF执行过程中，观测误差的有界性进行判断。因而，我们可以通过判断一个路标是否在现存路标的误差允许范围内来判断其是否为新的路标。路标区域可以通过图形绘制或者定义一个椭圆误差。

通过设定一个常数，最新观测到的路标可以通过下面的公式与之前观测到的路标相互关联。

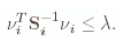其中，为观测新息，为特征的协方差矩阵。

9. 扩展卡尔曼滤波器(EKF)

在SLAM中，我们一般使用扩展卡尔曼滤波器基于机器人运动信息与传感器测量特征点信息估计机器人的状态。这里，我们将详细讨论将其应用于SLAM中的具体步骤。

在得到路标点的位置和方位，并且将路标点进行关联后，SLAM的过程分为如下三个部分：

1. 基于机器人运动信息更新机器人当前状态；

2. 基于路标信息更新估计状态；

3. 在当前状态中增加新的状态；

第一步相对来说较为简单，其仅仅需要将当前控制器的输出叠加到上一时刻的状态上。举例来说，假设机器人目前位于,当前运动信息为,那么第一部的机器人的当前状态为.

在第二步中，我们需要考虑路标信息，基于当前机器人的状态，我们可以估计路标应该处于的位置。这个估计位置与测量位置有所差别，这个差别被称作新息。新息即为机器人估计根据机器人状态估计信息与实际信息之间的差别。此时，根据上述新息，每个特征点的方法同时被更新。

在第三步中，观测到的新的路标被加入到状态中，即当前环境的地图。

下面我们对SLAM中常用的一些定义进行说明。

1.系统状态X

系统状态以及其协方差矩阵式SLAM过程中最为重要的向量。X包含了机器人的位置(x,y,\theta)以及环境中每个路标的信息。其格式如下图所示：

可以看出，系统状态X为一个(3+2*n)*1的矩阵，即列向量，其中n为路标的个数。其单位一般为米(m)或者毫米(mm)。角度一般选择为弧度。

2. 协方差矩阵P

两个变量之间的协方差矩阵描述的是两个变量之间的相关程度。

这里，协方差矩阵包含了机器人位置的协方差，路标的协方差以及机器人与路标之间的协方差。下图为协方差矩阵的一个形式。

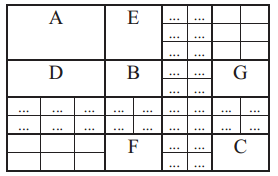
左上角第一个单元A描述的是机器人位置的协方差矩阵，其为一个3*3的矩阵。B为路标第一个路标的协方差矩阵，其为2*2的格式。C为最后一个路标的协方差矩阵。E机器人状态与第一个路标之间的协方差矩阵。D与E互为转置关系。可以看出，虽然协方差矩阵看起来较为复杂，但实际上其是有迹可循的。

在初始时刻，由于机器人并不知道任何路标的存在，因而P=A。初始化时，一般设置初始协方差矩阵为对角阵，反映的是初始位置的不确定性。虽然初始位置可能是精确的，单如果不包含初始误差，在之后的计算过程中可能会导致矩阵的奇异性。

3. 卡尔曼增益K

卡尔曼增益描述的是我们在估计系统真实状态时对观测值和计算值的信任程度。举例来说，假设我们通过计算得到机器人应该右移10cm，根据观测到的地标，我们可能发现机器人移动了5cm，因而此时我们就需要衡量机器人所处的真实位置。卡尔曼增益通过观测地标以及机器人运动估计的不确定性进行计算。如果测量元件精度相对于机器人运动估计，那么卡尔曼增益将会较小；反之较大。卡尔曼增益矩阵的形式如下图所示。

其中，第一列表示系统状态第一列的新息的增益。第一列前两行的元素表示位置新息增益，第三行表示角度新息增益。卡尔曼增益矩阵为(3+2n)*2的矩阵，其中n为地标数目。

4. 测量模型的雅可比矩阵H

测量模型的雅可比矩阵与测量模型息息相关。这里，我们首先讨论测量模型的构造。测量模型描述的是如何计算期望的位置和角度信息，它通过下面的过程计算得到：

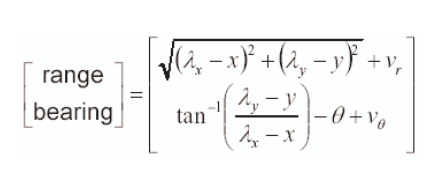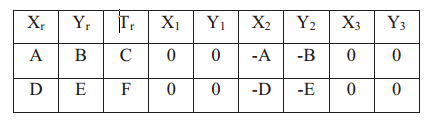其中，表示地标的x方向坐标；表示估计机器人位置；同理，表示地标的y方向坐标；y表示机器人的估计位置，为机器人方位角。通过上述公式我们便可以得到地标的位置和方位信息。其雅可比矩阵为：雅可比矩阵表示的地标的位置与方位角随着机器人位置和方位角变化的程度。第一行的第一个元素为地标位置相对于机器人x坐标的变化；第二个元素为相对于机器人y坐标的变化；最后一项为相对于机器人坐标的变化。可以看出，当机器人做纯旋转运动时，地标的位置并不发生变化。第二行表示的地标所处角度相对于机器人坐标变化的情况。上面的雅可比矩阵式我们使用EKF时常见的雅可比矩阵。在做SLAM时，我们通常需要一些额外的信息，如下：其中第一行仅用作指示，并不是矩阵的一部分。上面意味着前三列为常规雅可比矩阵。对于每一个地标，我们增加两列，其余为0，上图所示即为第二个地标的观测雅可比矩阵。

5. 预测模型的雅可比矩阵：A

与上述测量模型的雅可比矩阵一样，预测模型的雅可比矩阵与预测模型紧密相关，因而，这里我们首先考虑预测模型。预测模型表示的是如何根据机器人上一时刻的位置以及输出计算下一时刻的机器人的位置，其计算过程如下：

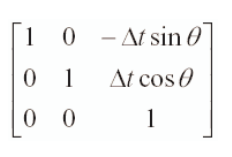其中，x和y为机器人位置，为机器人角度，为时间间隔，为误差项，因而，雅可比矩阵表示为：与上述观测矩阵计算方式一样，只不过我们现在增加了一列机器人角度列。由于预测方程仅用于机器人位置的预测，而与地标无关，因而雅可比矩阵相对比较简单。

6. SLAM特定的雅可比矩阵和

在SLAM中，还存在两个与常规EKF不同的雅可比矩阵，分别为和。其中，与预测模型雅可比矩阵基本一致，只不过，我们并不考虑机器人角度项，如下：

为地标预测模型的雅可比矩阵，但是只针对位置和角度，如下：
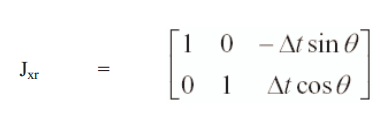
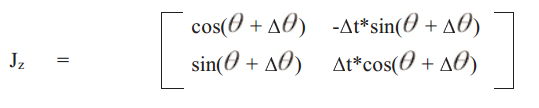7. 过程噪声Q和W

这里，我们假设系统中的噪声为高斯噪声，其幅值与控制幅值成正比。过程噪声的协方差矩阵为3*3的矩阵，如下所示：

其一般通过过程噪声进行自相关得到：

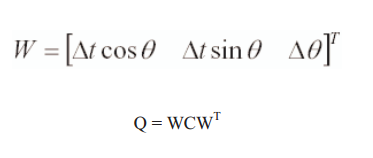
8. 测量噪声R和V

测量期间同样也假设包含高斯噪声。其协方差矩阵通过VRV^T计算得到，其中V为2*2的单位矩阵。其格式如下：

其中各元素表示测量期间的精度，精度越低，测量噪声越大；

10. SLAM的过程

1. 根据机器人运动信息预测机器人当前位置，使用下面方程实现：

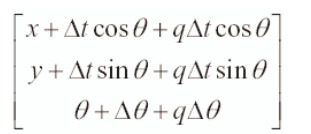此时，我们需要更新预测模型的雅可比矩阵以及预测误差向量如下图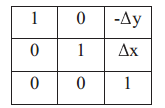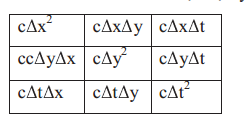：最后，我们需要计算当前机器人位置的新息，如下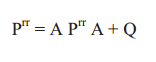：其中,表示P矩阵的前三列。

现在，我们拥有了机器人位置的预测值以及当前机器人位置估计的方差，接下来我们需要更新机器人的协方差矩阵，如下：

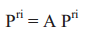2. 根据观测到的地标信息更新状态估计值

由于机器人运动模型的误差，在第一步中我们得到的机器人位置并不是机器人真实的位置，因而，我们需要通过观测值对上述估计进行修正。我们前面已经讨论了如何提取以及关联特征，这里不再讨论，使用机器人观测到的关联特征的变化，我们可以计算机器人的位移。进一步的，我们可以更新机器人位置的估计值。

这里，我们将根据当前机器人位置的估计值以及目前存储的地标位置利用下面的公式计算地标位置和角度的估计值：

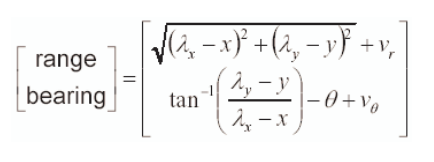通过对比上面计算得到的地标位置与测量得到的地标位置，我们可以计算此时的新息以及此时测量模型雅可比矩阵。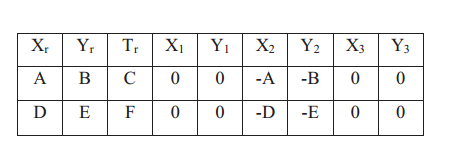根据前文所述，此时雅可比矩阵为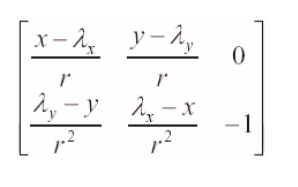：此时，同样我们需要更新误差矩阵R反映当前测量信息的不确定性。测量误差矩阵R的初始值可以设定为位置不确定性为1%,角度不确定性为1°。这里，误差不应该与测量值成正比。测量误差矩阵如下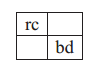：根据上面的计算，我们可以计算卡尔曼增益，其可以通过下面的方式计算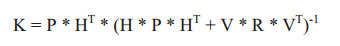：卡尔曼增益表示的是如何根据当前估计值与测量值更新当前的估计值。其中

被称作信息协方差S。

最后，我们可以使用上述卡尔曼增益计算一个新的状态向量。

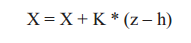上式将会更新当前机器人位置以及各个地标的位置。上述步骤对每一个地标均重复进行，直至对所有地标完成计算。

3. 为当前系统状态增加新的地标

这里，我们将在当前系统状态与协方差矩阵P中增加新的地标，目的是为了能够匹配更多的地标。

首先，我们可以按照下面的形式增加地标：

另外，我们需要在协方差矩阵中增加新的元素，如下图灰色部分所示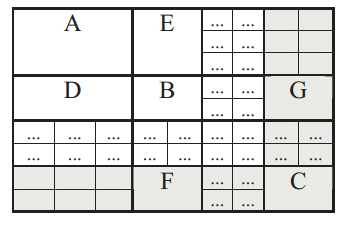：重复上述过程即完成了SLAM的所有过程。

10. 结语

上面提到的SLAM仅仅为非常基本的SLAM计算过程。SLAM目前仍然是研究的热点，其中有许多领域我们并没有提到，同样上述SLAM存在很大的提高余地。举例来说，机器人的闭环问题，即如何使机器人重新回到之前出现的地方。机器人应该能够识别出再次出现的地标并且使用最先出现的信息更新地标信息。另外，机器人应该在机器人回到一个已知地方之前更新地标信息。

另外，我们也可以将SLAM与网格方法相结合，将地图映射为人类可以读懂的格式另外，通过将SLAM与网格方法相结合，我们还可以进行机器人的路径规划。

参考文献：

本文大部分内容译自：

SLAM for Dummies- A Tutorial Approach to Simultaneous Localization and Mapping